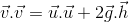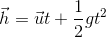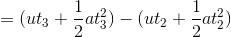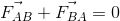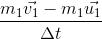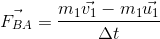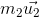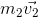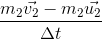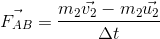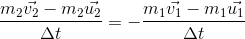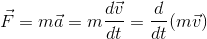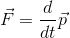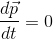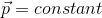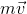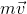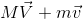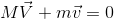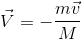IIT JEE(mains + advance )

Topics:
Motion in one dimension
A body
A certain amount of matter limited in all directions and consequently having a finite size, shape and occupying some definite space is called a body.
Particle
A particle is defined as a portion of matter infinitesimally small in size so that for the purpose of investigation, the distance between its different parts may be neglected. Thus, a particle has only a definite position, but no dimension. In the problems we are going to discuss, we will consider a body to be a particle for the sake of simplicity.
Motion
The position of object can change on a straight line (like on x-axis with respect to origin) or on a plane with respect to some fixed point on frame. So we can define motion as follows:-
An object or a body is said to be in motion if its position continuously changes with time with reference to a fixed point (or fixed frame of reference).
But note that, the moving object is either a particle, a point object (such as an electron) or an object that moves like a particle. A body is said to be moving like if every portion of it moves in the same direction and at the same rate.
Motion in One Dimension
When the position of object changes on a straight line i.e. motion of object along straight line is called motion in one dimension.
To understand the essential concepts of one dimensional motion we have to go through some basic definitions.
Frame of Reference
One can see the platform from a running train, and it seems that all the objects placed on platform are continuously changing their position. But one, who is on platform, concludes that the objects on the platform are at rest. It means if we will take the trains are reference frame the objects are not stationary and taking reference frame as platform the objects are stationary. So the study of motion is a combined property of the object under study and the observer. Hence there is a need to define a frame of reference under which we have to study the motion of an object.
Definition
A frame of reference is a set of coordinate axes which is fixed with respect to a space point (a body or an object can also be treated as a point mass therefore it can become a site for fixing a reference frame), which we have arbitrarily chosen as per our observer's requirement. The essential requirement for a frame of reference is that, it should be rigid.
Position of an Object
The position of an object is defined with respect to some frame of reference. As a convention, we define position of a point (essentially we treat body as a point mass) with the help of three co-ordinates X, Y and Z. Hence X, Y, Z is a set of coordinate axes representing a 3-dimensional space and each point in this space can be uniquely defined with the help of a set of X, Y and Z coordinate, all three axes being mutually perpendicular to each other. The line drawn from origin to the point represents the position vector of that point.
Position Vector
It describes the instantaneous position of a particle with respect to the chosen frame of reference. It is a vector joining the origin to the particle. If at any time, (x, y, z) be the Cartesian coordinates of the particle then its position vector is given by vector
= xi + yj + zk.
In one-dimensional motion: vector
= xi, y = z = 0 (along x-axis)
In two-dimensional motion: vector
= xi + yj (in x-y plane z = 0)
In the figure above, the position of a point P is specified and vector OP is called the position vector.
Displacement
Consider a case in which the position of an object changes with time. Suppose at certain instant 't' the position of an object is x1 along the x axis and some other instant 'T' the position is x1 then the displacement Δx is defined as,
Δx = x2 - x1
It can be seen in the figure above where x1 and x2 are instantaneous position of the object at that time.
Now consider the motion of a point A with respect to a reference point O. The motion of point A makes its radius vector vary in the general case both in magnitude and in direction as shown in figure above. Suppose the point A travels from point 1 to point 2 in the time interval Δt. It is seen from the figure that the displacement vector Δ
of the point A represents the increment of vector
in time Δt:
Δ
=
2 -
t
Difference Between Distance and Displacement
To understand the difference between distance and displacement, we study the motion of vertical throw of a ball with respect to point O, as shown in the left figure, to height h.
After some time it will come again to the same point O. The displacement of ball is zero but there is some distance traversed by the ball. It's because distance is a scalar quantity but displacement is a vector quantity.
Uniform and Non Uniform Motion
Speed is the rate of change of distance without regard to directions. Velocity is the rate at which the position vector of a particle changes with time. Velocity is a vector quantity whereas speed is scalar quantity but both are measured in the same unit m/sec.
The motion of an object may be uniform or non-uniform depending upon its speed. In case of uniform motion the speed is constant, whereas in the non-uniform motion, the speed is variable.
In uniform motion in one dimension the velocity (v) is mathematically defined as
v = (x2 - x1)/(T-t) ...... (1)
Where x1 and x2 are instantaneous displacement as shown in figure above at time 't' and 'T' respectively.
Graphical Representation of the Uniform Motion
Form the equation (1) we have the following equation
x2 = x1 + v(T - t)
where v is constant. Take t = 0, the equation becomes x2 = x1 + vT, from this equation it follows that the graph of position of object 'x2' against 'T' is a straight line, cutting off x1 on the position axis where x1 is the distance of the particle from the origin at time t = 0.
v = slope of the graph which is constant
Note:-
If the graph is not a straight line, it will represent non-uniform motion.
Motion of a body cannot be correctly identified unless one knows the position of body as specified by a fixed frame of reference.
Velocity Vector in Non Uniform Motion
In any non-uniform motion, we can define an average velocity over a time interval. Average velocity
is the ratio of the displacement Δx (that occurs during a particle time interval Δt) to that interval of time i.e.
Now refer to the example, related to figure 2.3, the ratio of Δ
/Δt is called the average velocity <
> during the time interval Δt. The direction of the vector <
> coincides with that of Δ
. Average velocity is also a vector quantity.
Note: The ratio of total distance traveled and time taken during the motion is called average speed. Average speed is a scalar quantity.
If at any time t1 position vector of the particle is
1 and at time
2 position vector is
2 then for this interval
Instantaneous velocity
Instantaneous velocity is defined as the rate of change of displacement.
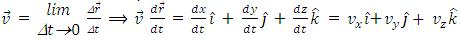
Velocity
The velocity at any instant is obtained from the average velocity shrinking the time interval closer to zero. As Δt tends to zero, the average velocity approaches a limiting value, which is the velocity at that instant, called instantaneous velocity, which is a vector quantity, mathematically we can define it as
The magnitude v of the instantaneous velocity is called the speed and is simple the absolute value of
In the example related with figure given below, the instantaneous velocity is
Hence instantaneous velocity is the rate at which a particle's position is changing with respect to time at a given instant. The velocity of a particle at any instant is the slope (tangent) of its position curve at the point representing that instant of time, as shown in figure above.
Speed
Speed is defined as rate of change of distance with time.
In any interval of time, average speed is defined as
= (total distance)/(total time taken) = Δs/Δt. As Δs > |Δ
|, hence >
Think : (i)Can a body have a constant speed and still have a varying velocity? (ii)Can a body have a constant velocity and still have a varying speed?
Problem 1:-
This question contains statement-1 (Assertion) and Statement-2 (Reason). Question has 4 choices (A), (B), (C) and (D) out of which only one is correct.
Statement-1
A bus moving due north take a turn and starts moving towards east with same speed. There will be no change in the velocity of the bus.
Statement-2
Velocity is a vector quantity.
(A) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for statement-1.
(B) Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for statement-1.
(C) Statement-1 is true, Statement-2 is false.
(D) Statement-1 is false, Statement-2 is true.
Solution:- (D)
This is so because bus is changing its direction of motion.
______________________________________________________________________________________________
Problem 2:-
A man started running form origin and went up to (2, 0) and returned back to (-1, 0) as shown in figure 2.7. In this process total time taken by man is 2 seconds. Find the average velocity and average speed.
Solution:-
The man is displaced form origin to (-1, 0)
Hence displacement, s =
So average velocity = Displacement/total time =
/2 = (-1/2)
m/sec.
where as, since the total distance traveled by man
= (0, 0) to (2, 0)+(2, 0) to (0, 0)+(0, 0) to (-1, 0)
= 2 + 2 + 1 = 5 m
Hence average speed
= (Total distance)/(Total time)=5/2 m/sec.
______________________________________________________________________________________________
Probem 3:-
A cyclist moves 12 km due to north and then 5 km due east in 3 hr. Find (a) his average speed, (b) average velocity, in m/s.
Solution:-
In the figure, A shows the initial position and C the final position of the cyclist. The total distance covered by the cyclist AB+BC= (12+5)km = 17 km.
So, its average speed = 17/3 km/hr = 1.57 m/s
Its displacement is AC and the magnitude is given by
AC = √(AB2 + BC2) = √(122 + 52) km = 13 km
Thus, its average velocity = 13/3 km/hr
= 1.2 m/s along AC, i.e at tan-1(5/12) or 22.6o East of North.
_______________________________________________________________________________________________
Problem 4:-
A train is moving with a constant speed of 5 m/s and there are two persons A and B standing at a separation of 10 m inside the train. Another person C is standing on the ground. Then, find
(a) displacement covered by A, if he moves towards B and back to its position in 10 seconds in frame of reference of train and in frame of reference of C.
(b) distance covered by A in frame of reference of train and in frame of reference of C.
Solution:-
(a) In the frame of train, displacement covered by A is zero and in frame of reference of C, displacement covered by A=0 + 5x10 = 50 m.
(b) Distance covered by A in frame of reference of train is 20m and distance covered by A in frame of reference of C is (20 + 50) = 70 m.
The dispalcement remains unaffected due to shifting of origin from one point to the other.
The displacement can have positive, negative or zero value.
The dispalcement is never greater than the actual distance travelled.
The displacement has unit of length.
Velocity can be considered to be a combination of speed and direction.
A change in either speed or direction of motion results in a change in velocity.
It is not possible for a particle to possess zero speed with a non-zero velocity.
A particle which completes one revolution, along a circular path, with uniform speed is said to possesss zero velocity and non-zero speed.
In case a body moves with uniform velocity, along a straight line, its average speed is equal to its instantaneous speed.
Acceleration
Acceleration is the rate of change of velocity with time. The concept of acceleration is understood in non-uniform motion. It is a vector quantity.
Average acceleration is the change in velocity per unit time over an interval of time.
Instantaneous acceleration is defined as
Acceleration Vector in Non Uniform Motion
Suppose that at the instant t1 a particle as in figure above, has velocity
and at t2, velocity is
. The average acceleration
during the motion is defined as
Variable Acceleration
The acceleration at any instant is obtained from the average acceleration by shrinking the time interval closer zero. As Δt tends to zero average acceleration approaching a limiting value, which is the acceleration at that instant called instantaneous acceleration which is vector quantity.
i.e. the instantaneous acceleration is the derivative of velocity.
Hence instantaneous acceleration of a particle at any instant is the rate at which its velocity is changing at that instant. Instantaneous acceleration at any point is the slope of the curve v (t) at that point as shown in figure above.
Equations of Motion
The relationship among different parameter like displacement velocity, acceleration can be derived using the concept of average acceleration and concept of average acceleration and instantaneous acceleration.
When acceleration is constant, a distinction between average acceleration and instantaneous acceleration loses its meaning, so we can write
where is the velocity at t = 0 and
is the velocity at some time t.
So,
.................. (2)
This is the first useful equation of motion.
Similarly for displacement
.................. (3)
in which
is the position of the particle at t0 and
is the average velocity between t0 and later time t. If at t0 and t the velocity of particle is
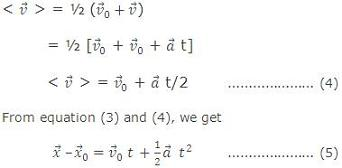
This is the second important equation of motion.
Now from equation (2), square both side of this equation we get
This is another important equation of motion.
Note:
The equation of motion derived above are possible only in uniformly accelerated motion i.e. the motion in which the acceleration is constant.
Refer this video for better understanding about motion in one dimension:-
Problem 5:-
The nucleus of helium atom (alpha-particle) travels inside a straight hollow tube of length 2.0 meters long which forms part of a particle accelerator. (a) If one assumes uniform acceleration, how long is the particle in the tube if it enters at a speed of 1000 meter/sec and leaves at 9000 meter/sec? (b) What is its acceleration during this interval?
Solution:-
(a) We choose x-axis parallel to the tube, its positive direction being that in which the particle is moving and its origin at the tube entrance. We are given x and vx and we seek t. The acceleration ax is not involved. Hence we use equation 3, x = x0 + t.
We get,
x = v0 + ½ (vx0) + vx) t, with x0 = 0 or
t = 2x/(vx0+vx),
t = ((2)(2.0 meters))/((1000+9000)meters/sec) = 4.0/10-4 sec Ans.
(b) The acceleration follows from equation 2, vx = vx0 + axt
=> ax = (v0-vx0)/t = ((9000-1000)meters/sec)/(4.0×10(-4) sec)
= 2.0 × 107 meter/sec2 Ans.
The above equations of motion are, however, universal and can be derived by using differential calculus as given below:
Thus, we have derived the same equation of motion using calculus.
To understand the use of calculus in solving the kinematics problems we can look into the following illustrations.
__________________________________________________________________________________________________
Problem 6:-
The displacement x of a particle moving in one dimension, under the action of a constant force is related to the time t by the equation t = √x + 3 where x is in meter and t is in seconds. Find the displacement of the particle when its velocity is zero.
Solution:-
Here t = √x + 3 => √x = t - 3
Squaring both sides, we get x = t2 - 6t + 9,
As we know velocity, v = dx/dt
Hence we get v = dx/dt = 2t - 6
Put v = 0, we get, 2t - 6 = 0
So,t = 3s
When t = 3s, x = t2 - 6t + 9 = 9 - 6(3) + 9 = 0
Hence the displacement of the particle is zero when its velocity is zero.
_________________________________________________________________________________________________
Problem 7:-
A particle starts from a point whose initial velocity is v1 and it reaches with final velocity v2, at point B which is at a distance 'd' from point A. The path is straight line. If acceleration is proportional to velocity, find the time taken by particle from A to B.
Solution:-
Here acceleration a is proportional to velocity v.
Hence a α v
=> a = kv, where k is constant
=> dv/dt = kv ............... (1)
=> (dv/ds)(ds/dt) = kv => (dv/ds) v = kv
=> k = (v2-v1)/d
From equation (1)
=> (dv/v)= k(dt)
or, ln (v2/v1) = kt
So, t = [ln (v2/v1)]/k = [d/(v2-v1)][ln (v2/v1)]
Question 1:-
What determines the nature of path following by the particle?
(a) speed (b) velocity (c) acceleration (d) none of these
Querstion 2:-
A moving body is covering distances in proportion to the square of time along a straight line. The acceleration of the body is:
(a) increasing (b) decreasing (c) zero (d) constant
Querstion 3:-
The distance covered by a body in time ‘t’ is propertional to the square of the time ‘t’. The acceleration of the body is:
(a) zero (b) constant (c) increasing (d) decreasing
Querstion 4:-
A train travels 4 km due east and then 3 km due north and finally comes back to the starting position travelling 5 km along south-west direction. What is the net displacement?
(a) 12 km (b) 5 km (c) zero (d) 1 km
Querstion 5:-
A body moves along a straight line, the motion of the body is said to be:
(a) one dimensional (b) two dimensional
(c) three dimensional (d) may be any of these three.
Q.1
Q.2
Q.3
Q.4
Q.5
a
d
b
c
d
Relative Velocity
In spite of our best efforts we could not find a fixed point with respect to which we should study absolute rest and absolute motion. So, the study of relative rest and relative motion assumes importance.
Consider two cars A and B running parallel to each other on same road with same velocities. No doubt the speedo meter of each indicates motion but the two drivers will always find themselves facing each other.
Relative velocity of a body A with respect to another body B, when both are in motion, is the velocity with which A appears to move to B.
The position, velocity and acceleration of a particle depend on the reference frame chosen.
A particle P is moving and is observed from two frames S and S'. The frame S is stationary and the frame S' is in motion.
Let at any time position vector of the particle P with respect to S is,
Position vector of the origin of S' with respect to S is,
From vector triangle OO'P, we get,
Physical Significance of Relative Velocity
Let two cars move unidirectional. Two persons A and B are sitting in the vehicles as shown in figure. Assume, VA = 10 m/s & VB = 4 m/s. The person A notices person B to be moving towards him with a speed of (10-4) m/s = 6 m/sec. That is the velocity of B with respect to (or relative to) A. That means
is directed from B to A.
Similarly A seems to move towards B with a speed 6 m/sec. That means the velocity of A relative to B (
) has the magnitude 6 m/sec & directed from A to B as shown in the figure.
Therefore,
In general,
So,
vAB = √ vA2 + vB2 - 2vAvB cosθ
and θ = tan-1{(vBsinθ)/(vA – vBcosθ)}
Relative Motion between Rain and Man
We know that, vr = vrg = velocity of rain w.r.t. ground, vm ≡ vmg.
Velocity of man w.r.t. ground and
velocity of rain w.r.t. man.
So,
That means the vector addition of the velocity of rain with respect of man (
) and the velocity of man (vehicle) (
) yield the actual velocity of rain
. The magnitude and direction of
can be given as,
vr = √((vrm)2+(vm)2+ 2vrm vm cosθ)
? = tan-1((vrm sinθ)/(vrm cosθ+ vm )) with horizontal
Illustration (JEE Main):
Four particles A, B, C and D are in motion. The velocities of one with respect to other are given as
is 20 m/s towards north,
is 20 m/s towards east and
is 20 m/s towards south. Then
is
(a) 20 m/s towards north
(b) 20 m/s towards south
(c) 20 m/s towards east
(d) 20 m/s towards west
Solution:
From the question, we know that,
…... (1)
…... (2)
…... (3)
Equation (1) – (2) + (3) gives:
or
That is,
is 20 m/s towards west.
Thus from the above observation we conclude that, option (d) is correct.
Illustration:
A stationary person observes that rain is falling vertically down at 30 km/hr. A cyclist is moving on the level road, at 10 km/hr. In which direction should the cyclist hold his umbrella to project himself from rain?
Solution:
Relative to stationary frame, velocity of rain is 30 km/hr downward. Take horizontal axis as x-axis and vertical axis as y-axis and i,j are the unit vectors along x and y axes respectively.
= 0-30j,
= 10î
= -30j - 10i = -10i - 30j
If angle between horizontal and
is θ, then,
tan θ = -30/-10 = 3
=> θ = tan-1 3 => θ=72° Therefore, to protect himself from rain the cyclist should hold the umbrella at an angle of 72° from horizontal.
Illustration:
A man walking eastward at 5 m/s observes that wind is blowing from the north. On doubling his speed eastward, he observes that wind is blowing from north-east. Find the velocity of the wind.
Solution:
Let velocity of the wind is,
vw=(v1i+v2j)m/s
And velocity of the man is,
vm=5i
So, vwm = vw- vm=(v1-5)i + v2j
In first case,
v1- 5 = 0 => v1= 5 m/s.
In the second case, tan 45o = v2/(v1- 10)
=> v2= v1 - 10 = -5 m/s.
=> vw= (5i - 5j) m/s.
Illustration:
From a lift moving upward with a uniform acceleration 'a', a man throws a ball vertically upwards with a velocity v relative to the lift. The ball comes back to the man after a time t.
Show that a + g = 2 v/t
Solution:
Let us consider all the motion from lift frame. Then the acceleration, displacement and velocity everything will be considered from the lift frame itself. As the ball comes back to the man, therefore displacement from the lift frame is zero. Again, the velocity with respect to the lift frame is v.
g - (-a) = a + g (↓) downwards
Now, s = ut + 1/2at2 => 0 = vt - 1/2 (a+g)t2
or a + g = 2(v/t) .
Relative Motion of a Swimmer in Flowing Water
Take
= velocity of man
= velocity of flow of river,
= velocity of swimmer w.r.t. river
can be found by the velocity addition of
and
.
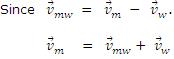
Crossing of the River with Minimum Drift
Case 1: vmw > w
A man intends to reach the opposite bank at the point directly opposite to the stationary point. He has to swim at angle θ with a given speed
w.r.t. water, such that his actual velocity
will direct along AB, that is perpendicular to the bank (or velocity of water
).
=> For minimum drift,
⊥
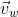
You can realize the situation by a simple example. If you want to reach the directly opposite point or cross the river perpendicularly, a man, that is to say, Hari, must report you that, you are moving perpendicular to the shore. What does this report signify? Since Hari observes your actual velocity (
) to be perpendicular to the bank
is perpendicular to
.
Observing the vector-triangle vw = vmw sinθ & vm = vmw cosθ
=> θ = sin-1 (vw/vmw ) & vm = √((vmw )2- (vw)2)
=> The time of crossing, t = d/vm
=> t = d/√(vmw )2 - (vw)2)
Case 2 : vw > vmw
Let the man swim at an angle θ’ with normal to the bank for minimum drift. Suppose the drift is equal to zero. For zero drift, the velocity of the man along the bank must be zero.
=> vm= vw- vmw sin θ' = 0
This gives, sinθ' = vw / vmw, since vw > vmw, sinθ' > 1 which is impossible. Therefore, the drift cannot be zero.
Now, let the man swim at an angle θ with the normal to the bank to experience minimum drift. Suppose that the drifting of the man during time t when the reaches the opposite bank is,
BC = x
x = (vm)x (t) … (1)
where t = AB/((vm )y cosθ) = d/(vmw cosθ) … (2)
and (vm)x = vw – vmw sin θ … (3)
Using (1), (2) & (3), we obtain
x = (vw- vmw sinθ d/(vmw cosθ))
= (vw/vmw sec θ-tanθ)d
x = (vw/vmw sec θ-tanθ)d … (4)
For x to be minimum,
dx/dθ = (vw/vmw secθ - tanθ - sec2θ)d = 0
vw/vmw tanθ = (sec θ) => sinθ = vmw/vw
θ = sin-1(vmw/vw)
Substituting the value of θ in (4), we obtain,
x = [√(vw2 – vmw2)/vmw] d
Refer this video for more about Relative Velocity
Crossing of the River in Minimum Time
Case 1: To reach the opposite bank for a given vmw
Let the man swim at an angle θ with AB. We know that the component of the velocity of man along shore is not responsible for its crossing the river. Only the component of velocity of man (vm) along AB is responsible for its crossing along AB.
The time of crossing = t = AB/(vmw cosθ)
Time is minimum when cos θ is maximum.
The maximum value of cos θ is 1 for θ = 0.
That means the man should swim perpendicular to the shore.
=>
mw ⊥
w
=> Then tmin = d/(vmw cosθ)|(θ=0) = d/vmw => tmin= d/vmw
Case 2:
To reach directly opposite point on the other bank for a given vmw & velocity v of walking along the shore.
To attain the direct opposite point B in the minimum time, let the man swim at an angle θ with the direction AB. The total time of journey t = the time taken from A to C and the time taken from C to B.
=> t = tAC + tCB
where tAC = AB/vmvcosθ & tCB = BC/v where v = walking speed of the man from C to B.
=> t = AB/vmvcosθ + BC/v
Again BC = (vm)xt
=> BC = (vw - vmwsinθ) (AB/vmwcosθ)
Using (1) & (2) we obtain,
t = AB/vmwcosθ + ((vw - vmwsinθ)/v(vmvcosθ))
=> t = AB[(1+vw/v)secθ/vmv - tanθ/v]
=> t = d/vmv[(1+vw/v)secθ/vmv - tanθ/v]
Putting dt/dθ = 0, For minimum t we get,
dt/dθ = d/dθ[d/vmv (1+vw/v) secθ/vmv - tanθ/v]
= [secθ/vmv - tanθ/v (1+vw/v) (sec2θ)/v] = 0
=>tanθ/vmv (1+vw/v) secθ/v
=> sin θ = (vmw/v+vw)
=> θ = sin-1(vmw/v+vw)
This expression is obviously true when vmw < v + vw.
Velocity of Separation/Approach, Relative Angular Velocity
Let thane be two particles A and B with velocity
and
at any instant as visualized from ground frame.
If we visualize the motion of B from frame of A the velocity of particle B would be
.
If α, β be the angle made with line AB,
then, VB cos β - VA cos α is relatively velocity of B w.r.t. A along line AB.
If VB cos β - VA cos α > 0; it is called as velocity of separation.
If VB cos β - VA cos α < 0; it is called as velocity of approach.
VB sin β - VA sin α is relative velocity of B w.r.t. A along direction perpendicular to AB. If length of AB is,
then, angular velocity B w.r.t. A is (VB sinβ - VA sinα)/l
and relative angular velocity = (VB sinβ - VA sinα)/l.


Question 1
A body dropped from a height h with initial velocity zero, strikes the ground with a velocity 3 m/s. Another body of same mass dropped from the same height h with an initial velocity of 4 m/s. Find the final velocity of second mass, with which it strikes the ground:
(a) 3 m/s (b) 4 m/s
(c) 5 m/s (d) 12 m/s
Question 2
From building two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically). If VA and VB are their respective velocities on reaching the ground, then:
(a) VB > VA (b) VA = VB
(c) VA> VB (d) their velocities depend on their masses
Question 3
If a car at rest accelerates uniformly to a speed of 144 km/h in 20 sec, it covers a distance of:
(a) 20 cm (b) 400 cm
(c) 1440 cm (d) 2980 cm
Question 4
A car, moving with a speed of 50 km/hr, can be stopped by brakes after atleast 6 m. If the same car is moving at a speed of 100 km/hr, the minimum stopping distance is:
(a) 12 m (b) 18 m
(c) 24 m (d) 6 m


| Q.1 | Q.2 | Q.3 | Q.4 |
c | b | b | c |
Circular Motion
Table of Content
Now we shall discuss another example of two-dimensional motion that is motion of a particle on a circular path. This type of motion is called circular motion.The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.
Direction of Motion of Body at any Instant
If the string breaks suddenly, the stone shall fly tangentially to the path of motion. So, instantaneous direction of motion of the body is always along the tangent to the curve at that point.
Consider a particle P is moving on circle of radius r on X-Y plane with origin O as centre.
The position of the particle at a given instant may be described by angle θ, called angular position of the particle, measured in radian. As the particle moves on the path, its angular position θ changes. The rate of change of angular position is called angular velocity, ω, measured in radian per second.
= dθ/dt = ds/rdt = v/r
The rate of change of angular velocity is called angular acceleration, measured in rad/s2. Thus, the angular acceleration is
α = dω/dt = d2θ/dt2
Relation Between these Parameters
It is easy to derive the equations of rotational kinematics for the case of constant angular acceleration with fixed axis of rotation. These equations are of the same form as those for on-dimensional transitional motion.
ω = ω0 + αt ............ (a)
? = ?0 + ω0t + αt2/2 ............ (b)
ω2 = ω02 + 2α (? - ?0) ............ (c)
? = ?0 + (ω0 + ω)/(2t) ............ (d)
Here, ?0 is the initial angle and ω0 is the initial angular speed.
Problem 1:
(a) What is the angular velocity of the minute and hour hands of a clock?
(b) Suppose the clock starts malfunctioning at 7 AM which decelerates the minute hand at the rate of 4Π radians/day. How much time would the clock loose by 7 AM next day?
Solution:-
(a) Angular speed of,
minute hand : ωmh = 2π rad/hr = 48π rad/day = (Π/1800) rad/sec
hour hand : ωhh = (π/6) rad/hr = 4π rad/day = (Π/21600) rad/sec
(b) Assume at t = 0, ?0 = 0, when the clock begins to malfunction.
Use equation (ii) to get the angle covered by the minute hand in one day.
So, ? = ω0(1 day) 1/2α(1 day)2 = 46π rad
Hence the minute hand complete 23 revolutions, so the clock losses 1 hour.
Problem 2:
A particle is rotating in a circular path having initial angular velocity 5 rad/sec and the angular acceleration α = 0.5 ω, where ω is angular velocity at that instant. Find the angular velocity, after it moved an angle π?
Solution:-
Here angular acceleration is
α = 0.5 ω
=> dω/dt = 0.5ω
=> (dω/dθ) (dθ/dt) = 0.5ω
=> ω dω/dθ = 0.5ω
Or,
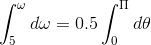
=> ω - 5 = 0.5 × π
=> ω = 5 + 0.5 ×π = 6.57 rad/sec.
Hence, when acceleration is not constant, use the method of calculus as shown in above illustration.
Simulation for Circular Motion’s Component
This animations shows the vectors components for any object traveling in a circle. (Radius vector, velocity vector, centripetal force vector and centripetal acceleration vector.) It then animates them traveling in a circle.
Motion of a Particle in a Circular Path
It is a special kind of two-dimensional motion in which the particle's position vector always lies on the circumference of a circle. In order to calculate the acceleration parameter it is helpful to first consider circular motion with constant speed, called uniform circular motion. Let there be a particle moving along a circle of radius r with a velocity
, as shown in figure given below, such that
= v = constant. For this particle, it is our aim to calculate the magnitude and direction of its acceleration. We know that,
Now, we have to find an expression for
in terms of known quantities. For this, consider the particle velocity vector at two points A and B. Displacing
, parallel to itself and placing it back to back with
, as shown in figure given below. We have
=
–
Consider ΔAOB, angle between OA and OB is same as angle between
and
because
is perpendicular to vector OA and
is also perpendicular to vector OB.
OB = OA = r and
So, ΔAOB is similar to the triangle formed by
,
and
Thus,From geometry we have, Δv/v = AB/r
Now AB is approximately equal to vΔt.
In the limit Δt → 0 the above relation becomes exact, we have
This is the magnitude of the acceleration. The direction
is instantaneously along a radius inward towards the centre of the circle, because of this
is called radial or centripetal acceleration. The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
Refer this video for better understanding about circular motion:-
Problem 3:
The moon revolved about the earth making a complete revolution in 2.36 mega second. Assume that the orbit is circular and has a radius of 385 mega meter. What is the magnitude of the acceleration of the moon towards the earth?
Solution:-
Here first of all we calculate speed v of the moon which is given by v = 2πR/T
where R = 385 mega meter = 385 × 106 m
and T = 2.36 mega second = 2.36 × 106 sec.
Hence v = 1020 m/sec.
The magnitude of centripetal acceleration is
a = v2/R = 0.00273 m/sec2.
From the above observation we conclude that, the magnitude of the acceleration of the moon towards the earth would be 0.00273 m/sec2.
In the previous enquiry we have discussed the uniform circular motion in which the particle has constant speed. If the particle's speed varies with time then the motion will be no more uniform but a non-uniform circular motion. Let us discuss about this motion using the concept of vectors.
Simulation for Car and Curves
This animation is used to explain why a passenger slides to the "outside" of a curve while riding inside a car is NOT an example of centrifugal forces. Instead is is a combination of centripetal force and inertia. It emphasize that when an object moves to the outside of a circle it is because of a lack of enough centripetal force and inertia keeps it moving in a straight line.
Non uniform circular motion:-
Let us use the vector method to discuss non-uniform circular motion.
In the side figure,
and
are unit vectors along radius and tangent vector respectively. In terms of er and eθ the motion of a particle moving counter clockwise in a circle about the origin in figure 2.30 can be described be the vector equation.
In this case, not only
but v also varies with time. We can obtain instantaneous acceleration as,
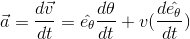
=(d
)/dt =
θ dθ/dt + v(d
θ)/dt
Again,
Here, aT = dv/dt and aR = v2/r
The first term,
is the vector component of
that is tangential to the path of the particle and arises from a change in the magnitude of the velocity in circular motion, called tangential acceleration whereas aR centripetal acceleration.
The magnitude of
is
Problem 4:
Point A travels along an arc of a circle of radius r as shown in figure given below. Its velocity depends on the arc coordinates l as v = A √l where A is a constant. Let us calculate the angle α between the vectors of the total acceleration and of the velocity of the point as a function of the coordinate l.
Solution:-
It is seen from figure shown above that the angle α can be found by means of the
formula tan α = aR/aT. Let us find aR and aT.
aR = v2/r=(A2 l)/r; aT= dv/dt = dv/dl = A/(2√l)×A√l = A2/2
Hence tan α = 2l/r.
Problem 5 (JEE Main):
Position vector of a particle moving in x-y palne at time t is
.
What will be the path of the particle?
Solution:-
x = a (1-cos ωt)
y = a sinωt
From first equation, we get
acos ωt = a-X …... (1)
From second equations, we get,
a sin ωt = y
Squaring and adding Eqs. (1) and (2), we get,
(X-a)2 + y2 = a2
This is an equation of a circle of radius a and ceter at (a,0).
Centripetal and centrifugal forces are equal in magnitude and opposite in direction.
Centripetal and centrifugal forces cannot be termed as action and reaction since action and reaction never act on same body.
Basic requirement for a body to complete motion in a vertical circle, under limiting conditions, is that the tension in the string must not vanish before it reaches the highest point. If it vanishes earlier, it will be devoid of the necessary centripetal force required to keep the body moving in a circle.
Cetrifugal force is the fictitious force which acts on a body, rotating with uniform velocity in a circle, along the radius away from the centre.
Question 1:-
When a body is moving in circular motion in a circular orbit at constant speed, it is in
(a) equilibrium (b) not in equilibrium
(c) unstable equilibrium (d) none of the above
Question 2:-
A body executes uniform circular motion
(a) its velocity is constant (b) its acceleration is constant
(c) its kinetic energy is constant (d) its velocity is zero
Question 3:-
In case of rigid body, the only possible type of internal motion is:
(a) linear (b) circular
(c) parabolic (d) hyperbolic
Question 4:-
When a body moves with a constant speed along a circle:
(a) its velocity remains constant (b) no force acts on it
(c) no work is done on it (d) no acceleration is produced in it.
Question 5:-
To move a body in a circle, which of the following forces is needed:
(a) centrifugal (b) gravitational
(c) centripetal (d) e.m.force
Q.1 Q.2 Q.3 Q.4 Q.5 a
c
b
c
c
While studying motion of bodies we have to keep two things in mind. We have to study various characteristics associated with moving bodies while we are to explore and study in detail, about the cause of producing motion. Kinematics is the branch of physics which deals only with the description of motion of bodies. Mainly there are two type of graphs are belonging to the kinematics. One is position-time graph and the other is velocity-time graph.
These graphs will have validity only if motion under study is along a straight line. Then, displacement, velocity and acceleration vectors are collinear and can be treated as algebraic quantities. Let x-axis be the path of motion. Then, x-coordinate represents the magnitude of position vector.
Position - Time Graph
If we plot time t along the x-axis and the corresponding position (say x) from the origin O on the y-axis, we get a graph which is called the position-time graph. This graph is very convenient to analyse different aspects of motion of a particle. Let us consider the following cases.
(i) In this case, position (x) remains constant but time changes. This indicates that the particle is stationary in the given reference frame. Hence, the straight line nature of position-time graph parallel to the time axis represents the state of rest. Note that its slope (tan θ) is zero.
(ii) When the x-t graph is a straight line inclined at some angle (θ≠) with the time axis, the particle traverses equal displacement Δx in equal intervals of time Δt. The motion of the particle is said to be uniform rectilinear motion. The slope of the line measured by Δx/Δt = tθ represents the uniform velocity of the particle.
(iii) When the x-t graph is a curve, motion is not uniform. It either speeds up or slows down depending upon whether the slope (tan θ successively increases or decreases with time. As shown in the figure the motion speeds up from t = 0 to t=t1 (since the slope tan θ increases). From t=t1 to t=t2, AB represents a straight line indicating uniform motion. From t=t2 to t=t3, the motion slows down and for t>t3 the particle remains at rest in the reference frame.
Problem 1:-
The adjacent figure shows the displacement-time graph of a particle moving on the x-axis. Choose the correct option given below.
(A) The particle is continuously going in positive x direction.
(B) The particle is at rest.
(C) The particle moves at a constant velocity upto a time t0, and then stops.
(D) The particle moves at a constant acceleration upto a time t0,and then stops.
Solution:
The correct option is (C). Up to time t0, particle is said to have uniform rectilinear motion and after that comes to rest as the slope is zero.
The Velocity - Time Graph
The velocity-time graph gives three types of information.
(i) The instantaneous velocity.
(ii) The slope of the tangent to the curve at any point gives instantaneous acceleration.
a = dv/dt = tan θ
(iii) The area under the curve gives total displacement of the particle.
Now, let us consider the uniform acceleration. The velocity-time graph will be a straight line.
The acceleration of the object is the slope of the line CD.
a = tan θ = BC/BD = (v-u)/t
v = u +at …... (1)
The total displacement of the object is area OABCD
s = Area OABCD = Area of rectangle OABD + Area of triangle BCD
s = ut + (1/2)at2 …... (2)
Again, s = Area OABCD
= 1/2(AC + OD) x OA = 1/2(v + u)xt
Problem 2:-
From the velocity-time plot shown in figure, find
(a)distance travelled by the particle during the first 40 seconds.
(b)displacement travelled by the particle during the first 40 seconds.
(c) Also find the average velocity during the period.
Solution:
(a) Distance = area under the curve = 1/2 x 20 x 5 + 1/2 x 5 x 20
For distance measurement, the curve is plotted as in Fig. (a)
(b) Displacement = area under the curve in Fig. (b) = 0
(c) Vav = Displacement/time
As displacement is zero,
Thus, Vav = 0
Therefore average velocity during the period will be zero.
Problem 3 (JEE Main)
Two cars A and B cross a point P with velocities 10 m/s and 15 m/s. After that they move with different uniform accelerations and the car A overtakes B with a speed of 25 m/s. Find out the velocity of B at that instant?
Solution:
Let aA = a1 and aB = a2
(25)2 = (10)2+2a1S
Or, 2a1S = 525 ….... (1)
25 = 10+a1t
So, a1t = 15 …... (2)
Let velocity of B at that instant is v. Then
v2 = (15)2+2a2S
Or, 2a2S = v2-225 …... (3)
v = 15+a2t
So, a2t = v – 15 …... (4)
From equations (1) and (2),
2S/t = 525/15 = 35
and from equations (3) and (4),
2S/t = v2-225/v-15
So, 35 = v2-225/v-15
Solving these two equations we get,
v = 20 m/s
Therefore from the above observation we conclude that, the velocity of B at that instant would be 20 m/s.
Problem 4:-
The velocity-time graph of a moving object is given in the figure. Find the maximum acceleration of the body and distance travelled by the body in the interval of time in which this acceleration exists.
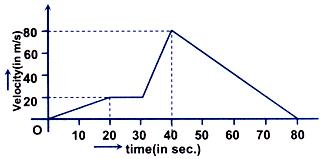
Solution:
Acceleration is maximum when slope is maximum,
amax = (80-20)/(40-30) = 5m/s2
S = 20 m/s x 10 s + 1/2 x 6 m/s2 x 100s2 = 500m
Problem 5:-
The displacement versus time curve is given:
Column I Column II
(a) OA (p) Velocity increase with time linearly
(b) AB (q) Velocity decreases with time
(c) BC (r) Velocity is independent of time
(d) CD (s) Velocity is zero
Solution:
(a) → (p) (b) → (r) (c) → (q) (d) → (s)
This is so because slope of displacement-time curve gives instantaneous velocity.
Refer this video for better understanding about equation of motion:-
The acceleration-time graph:-
Acceleration time curves give information about the variation of acceleration with time. Area under the acceleration time curve gives the change in velocity of the particle in the given time interval.
Refer this simulation that shows a car traveling along a graph:-
The purpose is to show that, the car can traverse the graph, then it's first derivative is a continuous function.
The displacement can have positive, negative or zero value.
The displacement is never greater than the actual distance travelled.
A change in either speed or direction of motion results in a change in velocity.
It is not possible for a particle to possess zero speed with a non-zero velocity.
The velocity-time graph for a uniformly accelerated body is a straight line.
Question 1:-
The position-time graph of a body is parallel to t-axis. The body is said to be moving with:
(a) uniform velocity (b) non-uniform velocity
(c) may be uniform or npn-uniform velocity (d) no motion at all
Question 2:-
The relation between time t and distance x is t = ax2+bx, where a and b are constants. The acceleration is:
(a) 2bV3 (b) -2abV2
(c) 2aV2 (d) -2aV3
Question 3:-
A car has to cover the distance 60 km, if half of the total time it travels with velocity 80 km/h and in rest half time its speed becomes 40 km/h, the average speed of car will be,
(a) 60 km/h (b) 80 km/h
(c) 120 km/h (d) 180 km/h
Question 4:-
In a straight line motion the distance travelled is propertional to the square root of the time taken. The acceleration of the particle is proportional to:
(a) velocity (b) V2
(c) V3 (d) √V
Question 5:-
The displacement of a particle along a straight line at time t is given by x = b0+b1t+b2t2. The acceleration of the particle is:
(a) b0 (b) b1
(c) 2b2 (d) b2/2
Q.1 Q.2 Q.3 Q.4 Q.5 d
d
a
c
c
Table of Content
Now we discuss some example of curved motion or two dimensional motion of constant acceleration such as the motion of constant acceleration such as the motion of a particle projected at certain angle with the horizontal in vertical x-y plane (this type of motion is called projectile motion). Air resistance to the motion of the body is to be assumed absent in this type of motion.
A body projected into the space and is no longer being propelled by fuel is called a projectile.
To analyze the projectile motion we use the following concept "Resolution of two dimensional motion into two one dimension motion" as discussed earlier. Hence it is easier to analyze the motion of projectile as composed of two simultaneous rectilinear motions which are independent of each other:
(a) Along the vertical y-axis with a uniform downward acceleration 'g' and
(b) Along the horizontal x-axis with a uniform velocity forward.
Consider a particle projected with an initial velocity u at an angle θ with the horizontal x-axis as shown in figure shown below. Velocity and accelerations can be resolved into two components:
Velocity along x-axis = ux = u cos θ
Acceleration along x-axis ax = 0
Velocity along y-axis = uy = u sin θ
Acceleration along y-axis ay = -g
Here we use different equation of motions of one dimension derived earlier to get the different parameters.
…... (a)
…... (b)
v2 = v02 – 2g (y-y0) …... (c)
Total Time of Flight
When body returns to the same horizontal level, the resultant displacement in vertical y-direction is zero. Use equation b.
Therefore, 0 = (u sin θ) t - (½)gt2,
As t cannot equal to zero, then, total time of flight,
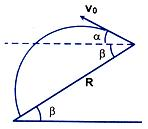
Horizontal Range
Horizontal Range (OA=X) = Horizontal velocity × Time of flight
= u cos θ × 2 u sin θ/g
So horizontal range,
Maximum Height
At the highest point of the trajectory, vertical component of velocity is zero.
Therefore, 0 = (u sin θ)2 - 2g Hmax
So, maximum height would be,
Refer this video for better understanding about projectile motion:-
Equation of Trajectory
Assuming the point of projection as the origin of co-ordinates and horizontal direction as the x-axis and vertical direction as the y-axis. Let P (x, y) be the position of the particle at instant after t second.
Then x = u cos θ.t and y = u sin θ.t - 1/2 gt2
Eliminating 't' form the above equations, we get,
y = x tan θ - (gx2/2u2cos2θ)
This is the equation of trajectory which is a parabola (y = ax + bx2).
Refer this simulation for projectile motion:-
A ball is launched at an angle and lands at the same height it is launched from. A camera takes a picture of the flight every second on the same frame of film. The images are then moved down and to the right to show the independence of horizontal and vertical motion.
Problem 1 (JEE Advanced)
The speed of a projectile when it is at its greatest height is √2/5 times its speed at half the maximum height. Find out the angle of projection.
Solution :-
Let θ be the angle of projection and u its initial speed. Then maximum height will be,
H = u2sin2θ/2g
So, gH = u2sin2θ/2
Now, vH = u cosθ
Or, vH2 = u2 cos2θ …... (1)
vH/22 = u2-2g(H/2) = u2-gH
vH/22= u2-(u2sin2θ/2) …...(2)
Now it is given that,
vH = [√2/5] vH/2
Or, vH2 = (2/5) vH/22
Substituting the values from equations (1) and (2), we get,
(u2 cos2θ) = 2/5 [u2-(u2sin2θ/2)]
Or, 5cos2θ = 2[1-(sin2θ/2)]
Or, 5(1-sin2θ) = 2-sin2θ
Or, sin2θ = ¾
Or, sinθ = (√3)/2, Or, θ = 60o
Thus from the above observation, we conclude that, the angle of projection would be 60o.
Problem 2:-
A gun moving at a speed of 30m/sec fires at an angle 30o with a velocity 150m/s relative to the gun. Find the distance between the gun and the projectile when projectile hits the ground. (g = 10 m/sec)
Solution :-
Vertical component of velocity = 150 sin 30o = 75 m/sec
Horizontal component of velocity relative to gun = 150 cos 30o = 75√3 m/sec
Horizontal component of velocity relative to ground = 75√3 + 30 ≈ 160m/sec
Time of flight = (2
75)/g = 15 s
Range of projectile = 160 × 15 = 2400 m
Distance moved by the gun and projectile = 2400 - 450 = 1950 m.
Horizontal Projection:-
Consider a particle projected horizontally with a velocity
from a point O as shown in side figure.
Assuming the point of projection O as the origin of coordinates and horizontal direction as the X-axis and vertical direction as Y-axis. Let P (x, y) be the position of the particle after t seconds.
So, x = horizontal distance covered in time t = ut. ............... (1)
y = vertical distance covered in time t = ½gt2 ............... (2)
Eliminate t from equations (1) and (2) then we get,
y = (1/2)(g/u2) (x2)
This is the equation of parabola passing through the origin, with its vertex at the origin O. Hence the trajectory is a parabola.
Problem 3:-
A stone is thrown at a speed of 19.6 m/sec at an angle 30o above the horizontal from a tower of height 490 meter. Find the time during which the stone will be in air. Also find the distance from the foot of the tower to the point where stone hits the ground?
Solution :-
Let us consider the motion of stone in the horizontal and vertical directions separately.
(i) Vertical motion (downward direction negative) :
Initial vertical velocity y = 19.6 sin 30o
Acceleration a = g = -9.8 m/s2
Vertical distance covered = h = 490 m
Using, h = ut + 1/2gt2
We have, 490 = - 9.8t + (1/2) 9.8t2
100 = - 2t + t2 or t2 - 2t - 100 = 0
t = 11.05 sec
(ii) Horizontal motion:
Initial horizontal velocity y = 19.6 sin 30o = 9.8 m/s
Hence distance from the foot of tower to the point where stone hits the ground
= Horizontal component × time of flight
= 19.6 cos 30o × 11.05 = 188 m
Projectile Motion on an inclined plane:-
Let the particle strike the plane at A so that OA is the range of the projectile on inclined plane. This initial velocity
can be resolved into two components:
(i) u cos (α - β) along the plane
(ii) u sin (α - β) perpendicular to the plane.
The acceleration due to gravity g can be resolved into two components:
(i) g sin β parallel to the plane
(ii) g cos β perpendicular to the plane.
Time of Flight:-
Let t be the time taken by the particle to go from A to B. In this time the displacement of the projectile to the plane is zero.
Hence, 0 = u sin (α-β) t - ½g β t2
=> t = 2u sin(α-β)/gcosβ
Range:-
During time of flight, the horizontal velocity u cos α remains constant.
Hence, horizontal distance,
OB = (ucosα) t = 2u2sin(α-β)cosα/gcosβ
Now, OA = OB/cosβ = 2u2sin(α-β)cosα/gcosβ
The greatest distance of the projectile from the inclined plane is u2sin2 (α-β)/2gcosβ .
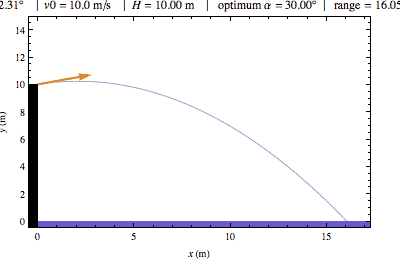
Problem 4:-
A Particle is projected with a velocity 39.2 m/sec at an angle of 30o to an inclined plane (inclined at an angle of 45o to the horizontal). Find the range on the incline (a) when it is projected upward (b) when it is projected downward.
Solution :-
Time of flight will be same in both cases because the acceleration perpendicular to the plane is same. Therefore,
0 = 39.2 sin 30o t - (½) g cos 45o t2
Or, t = (2×39.2 sin 30)/(g cos 45) = 4√2 sec
(a) Range upward
= 39.2 cos 30o t - (½) g sin 30o t2
= 39.2 × √3/2 × 4√2- (1/2) × 9.8 × (1/2) × (4√2)2 = 113.7m
(b) Range downward
= 39.2 cos 30o × t + (½) g sin 30o t2
= 39.2 × √3/2 × 4√2 + (1/2) × 9.8 × (1/2) × (4√2)2 = 270.5m Ans.
Motion down the plane:-
Let the particle be thrown at a velocity v0 at angle ‘α’ with the horizontal as shown in figure.
v0 sin (α+β)T- 1/2 gcosβT2=0 [for y'=0]
=> T = (2v0 sin(α+β))/gcosβ
R = v0 cos(α+ β)T+ 1/2 g sin βT2= (v02)/g [(sin(2α+β)+sinβ)/(1-sin2β)]
Since α is the variable and maximum value of sin function is 1, therefore for R to be maximum, sin (2α+β)=1
and Rmax (v02)/g [(1+sinβ)/(1-sin2β)]= (v02)/(g(1-sinβ)) down the plane.
Every projectile experiences one single force and that is due to gravity only.
Horizontal velocity of a projectile remains the same throughout its flight (it may be zero also).
No projectile ever experiences any acceleration in the horizontal direction.
Vertical acceleration of every projectile is ‘-g’.
The path of projectile is parabolic except for those projected along vertical direction. In that case it is a straight line.
The horizontal and vertical motion of a projectile are independent of each other.
Question 1:-
Which of the following is not a projectile:
(a) a bullet fired from a rifle (b) a bomb dropped from an aeroplane
(c) a cricket ball moving in space (d) hydrogen balloon floating in air
Question 2:-
A particle projected horizontally from the top of a tower clears range equal to the height of a tower. The path described is a part of a:
(a) circle (b) ellipse
(c) hyperbola (d) parabola
Question 3:-
A particle is thrown vertically upward. At its highest point, it has:
(a) an upward velocity (b) downward velocity
(c) an upward acceleration (d) a downward acceleration
Question 4:-
A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s, then maximum height attained by it:
(a) 8 m (b) 20 m
(c) 10 m (d) 16 cm
Question 5:-
A body is projected horizontally from the top of a tower 19.6 meter high. It reaches the ground in:
(a) 1 sec (b) 2 sec
(c) 2.5 sec (d) 5 sec
Q.1 Q.2 Q.3 Q.4 Q.5 b
d
d
c
b
Table of Content
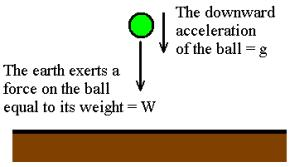
Whenever a body is released frrom a height, it travels vertically downward towards the surface of earth.This is due to the force of gravitational attraction exerted on body by the eareth. The acceleration produced by this force is called acceleration due to gravity and is denoted by ‘g’. Value of ‘g’ on the surface of earth is taken to the 9.8 m/s2 and it is same for all the bodies. It means all bodies (whether an iron ball or a piece of paper), when dropped (u=0) from same height shoulfd fall with same rapidity and should take same time to reach the earth. Our daily observation is contrary to this concept. We find that iron ball falls more rapidlly than piece of paper. This is due to the presence of air which offers different resistance to them. In the absence of air both would have taken same time to reach the surface of earth.
When a body is dropped from some height (earth's radius = 6400 km), it falls freely under gravity with constant acceleration g (= 9.8 m/s2) provided the air resistance is negligible small. The same set of three equations of kinematics (where the acceleration
remains constant) are used in solving such motion. Here, we replace
by
and choose the direction of y-axis conveniently. When the y-axis is chosen positive along vertically downward direction, we take
as positive and use the equation as
v = u + gt, v2 = u2 + 2gh, and h = ut + 1/2gt2
where h is the displacement of the body and u is initial velocity of projection in the vertically downward direction. However, if an object is projected vertically upward with initial velocity u, we can take y-axis positive in the vertically upward direction and the set of equations reduces to
v = u - gt, v2 = u2 - 2gh, and h = ut - 1/2gt2
In order to avoid confusion in selecting
as positive or negative, it is advisable to take the y-axis as positive along vertically upward direction and point of projection as the origin. We can now write the set of three equations in the vector form:
,
and
where h is the displacement of the body.
Problem:
The motion of a particle is described by the equation u = at. The distance travelled by the particle in the first 4 second.
Solution:
Because for the motion u = at. So acceleration is uniform which is equal to a.
Therefore, Distance traveled = 1/2[(a)(4)2] = 8a
Problem:
A body moving with a constant retardation in straight line travels 5.7 m and 3.9 m in the 6th and 9th second, respectively. When will the body come momentarily to rest?
Solution:
A body moving with initial velocity u and acceleration a, traverses distance Sn in nthsecond of its motion.
Sn = u + (1/2)(2n - 1)a => 5.7 = u + (1/2)(2 x 6 - 1) a
or 5.7 = u + (11/2) a
and 3.9 = u + (1/2)(2 x 9 - 1)a or, 3.9 = u + (17/2) a
Solving eqns. (1) and (2) we get, u = 9 m/s and a = -0.6 m/s2.
If the body stops moving after t seconds, then from the relation v=u+at
Thus, 0 = 9 + (-0.6)t or, t = (9/0.6)s = 15s
Problem (JEE Advanced):
A stone, thrown up is caught by the thrower after 6s. How high did it go and where was it 4 s after start? g = 9.8 m/s2
Solution:
Time to go up and come back = 6s
Thus, time to reach the highest point = (6/2) s = 3s
From point of projection to the highest point we have
u = ?, v = 0, a = -9.8 m/s2, t = 3s
Using the relation, v = u + at
0= u – 9.8
3
Thus, u = 29.4 m/s2
Maximum height, H = u2/2g = [(29.4)2/2(9.8)] m =44.1 m
Let h = height of stone at 4s.
Using the relation, S = ut + ½ at2
So, h = [(29.4)(4)-1/2 (9.8) (4)2]m
= [117.6-78.4] m = 39.2 m
From the above observation we conclude that, the height would be 39.2 m.
Refer this video to know more about, “Motion Under Gravity”.
Problem:
A car moving in a straight line at 30 m/s slows uniformly to a speed of 10 m/s in 5 sec. Determine:
(a)the acceleration of the car,
(b)displacement in the third second.
Solution:
Let us take the direction of motion to be the +x direction.
(a) For the 5 s interval, we have t = 5 s, u = 30 m/s, v = 10 m/s
Using v = u + at, we have
a = (v-u)/t = (10-30)/5 = -4 m/s2
(b) s = (displacement in 3s) - (displacement in 2s)
Here u = 30 m/s, a = -4 m/s2, t2 = 2 s; t3 = 3 s
s = 30(3-2) + 1/2(-4)(32-22) = 20 m
Alternatively
Sn = u + a/2(2n - 1)
Hence n = 3,
Therefore, s3 = 30 + ((-4))/2 [(3)- 1]= 20 m
Problem:
A bullet fired into a fixed target loses half of tis velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion.
Solution:
Let initial velocity of the bullet = u
After penetrating 3 cm its velocity becomes = u/2
From v2 = u2 - 2as
(u/2)2 = u2 - 2as
Thus, a = u2/8
Let further it will penetrate through distance x and stops at some point.
0 = (u/2)2 - 2 (u2/8)x
Therefore, x = 1 cm
Problem:
An anti-aircraft shell is fired vertically upwards with a muzzle velocity of 294 m/s. Calculate (a) the maximum height reached by it, (b) time taken to reach this height, (c) the velocities at the ends of 20th and 40th second. (d) When will its height be 2450 m? Given g = 9.8 m/s2.
Solution:
(a) Here, the initial velocity u = 294 m/s and g = 9.8 m/s2
Thus, the maximum height reached by the shell is,
H = us/2g = 2942/(2 x 9.8) = 4410 m = 4.41 km
(b) The time taken to reach the height is, T = u/g = 294/9.8 = 30 s
(c) The velocity at the end of 20th second is given by
v = u - gt = 294 - 9.8 x 20 = 98 m/s upward,
and the velocity at the end of 40th second is given by,
v = 294 - 9.8 x 40 = -98 m/s
The negative sign implies that the shell is falling downward.
(d) From the equation,
H = ut + (1/2)gt2 or 2450 = 2941 t - 1/2 x 9.8 t2
or t2 - 60 t + 500 = 0
Therefore, t = 10 s and 50 s.
At t = 10 s, the shell is at a height of 2450 m and is ascending, and at the end of 50 s it is at the same height, but is falling.
Acceleration of all these bodies is constant.
Acceleration is always directed downward.
All bodies, when dropped (u=0) from same height should fall with same rapidity and should take same time to reach the earth.
Question 1
A stone is released with zero velocity from the top of a tower reaches the ground in 4 second, the height of the tower is about
(a) 20 m (b) 40 m
(c) 80 m (d) 16 m
Question 2
A stone is thrown vertically upwards with an initial velocity of 30 m/s. The time taken for the stone to rise to its maximum height is
(a) 0.326 s (b) 3.26 s
(c) 30.6 s (d) 3.06 s
Question 3
Two balls are dropped from same height at 1 second interval of time. The separation between the two balls after 3 seconds of the drop of first ball is:
(a) 50 m (b) 40 m
(c) 35 m (d) 25 m
Question 4
A ball takes t second to fall from a height h1 and 2t seconds to fall from a height h2. Then h1/h2 is:
(a) 0.5 (b) 0.25
(c) 2 (d) 4
Q.1 Q.2 Q.3 Q.4 c
d
d
b
Newton’s Laws of Motion
Table of Content
Newton's laws of motion are of fundamental importance in classical physics. Newton gave three laws connected with motion and are, popularly, known as Newton’s laws of motion.
(a) First Law (Law of Inertia)
Everybody continues in its state of rest or of uniform motion in a straight line unless it is compelled by some external force to change that state.
(b) Second Law
The rate of change of momentum of a body is directly proportional to the impressed force and takes place in the direction of the force.
So, F= dp/dt
This results force acting a body F is equal to the mass of the body m times acceleration of the body a.
So, F = ma
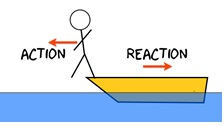
(c)Third Law
To Every action there is an equal and opposite reaction.
FAB = - FBA
The first two laws relate to the type of motion of a system that results from a given set of forces. The third law studies the basic nature of all forces i.e. they act in action - reaction pair.
"Newton's laws of Motion" is one of the easiest and important chapters of Mechanics in the Physics syllabus of IIT JEE, AIEEE and other engineering examinations. These laws are not new to any aspirant as he is using these laws even in previous classes. The examples based on this are very easy and can be seen even in day to day life.
The chapter is important not only because it fetches 2-3 questions in most of the engineering examination but also because it is prerequisite to the other chapters of Mechanics.
Following topics are covered under Newton’s Laws of motion:
Laws of motion is important from the perspective of scoring high in IIT JEE as there are few fixed pattern on which a number Multiple Choice Questions are framed on this topic. You are expected to do all the questions based on this to remain competitive in IIT JEE examination. It is very important to master these concepts at early stage as this forms the basis of your preparation for IIT JEE, AIEEE, DCE, EAMCET and other engineering entrance examinations.
Conservation of Linear Momentum
Table of Content
It states that,
“In an isolated system (no external force), the algebraic some of the momenta of bodies, along any straight line, remains constant and is not changed due to their mutual action and reaction on each other”.
This can be verified by a following simple experiment.
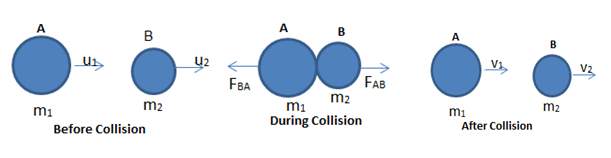
Consider a body ‘A’ of mass ‘m1’ moving with a velocity
strike against another body ‘B’ of mass m2,moving with velocity in same direction as shown in the below figure. Two bodies remain in contact with each other for small time ‘?t’. They get separated and move with velocities
and
after collision.
Let
be the force exerted by ‘A’ upon ‘B’ and
be its reaction. Since the system is isolated, i.e., no external force is there,
So,
…... (1)
This is in accordance with Newton’s third law of motion that ‘action and reaction are equal and opposite’.
Considering the momenta of the bodies before and after collision.
Body A
Body B
Momentum of A before collision =
Momentum of A after collision =
Change in momentum of A =
Time taken for the change of momentum =?t
Rate of change of momentum of A (=Force on A) =
So,
Momentum of A before collision =
Momentum of B after collision =
Change in momentum of B =
Time taken for the change of momentum =?t
Rate of change of momentum of B (=Force on B)=
So,
Substituting for
and
in equation (1),
Or,
Thus, the total momentum of the system before collision is equal to the total momentum of the system after collision.
This verifies the law of conservation of momentum.
It may be noted that the conservation of momentum is closely connected with the validity of Newton’s third law of motion, since we have used equation (1) [which is nothing but third law] to prove it.
Alternative Method
According to Newton’s second law of motion,
Since
(momentum of body),
Incase of an isolated system,
Thus,
or,
Therefore, momentum (in vector form) of an isolated system remains constant. This is in accordance with the law of conservation of momentum.
IMPORTANT NOTE:-
While applying law of conservation of momentum to a system following consideration must be kept in mind:
(a) The system must be isolated.
(b) While finding the algebraic sum of momenta it must be ensured that all of them are along a particular straight line.
Applications of Conservation of Momentum
Following few examples with illustrate the law of conservation of momentum.
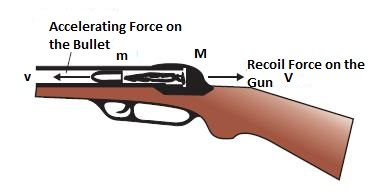
(a) Recoil of Gun
A gun and a bullet constitute one isolated system. On firing the gun, bullet moves out with a very high velocity
. The gun experiences a recoil. It moves in the opposite direction as shown in the below figure. Velocity ‘
’ of the recoil gun can be calculated by the application of law of conservation of momentum.
Before Firing
After Firing
Momentum of bullet = 0
Momentum of gun = 0
Total momentum of the system = 0
Momentum of bullet =
Momentum of gun =
Total momentum of the system =
Here ‘m’ and ‘M’ are the masses of bullet and gun respectively. According to the law of conservation of momentum, momentum before collision and after collision must be same.
or,
or,
Negative sign indicates that direction of motion of gun is in opposite direction.
(b) Rocket and Jet Plane
Fuel and oxygen is burnt in the ignition chamber. As hot gases escape from a rear opening, with some momentum, the rocket moves in the forward direction with the same momentum.
(c) Explosion of a Bomb
Momentum of a bomb before explosion is zero. After explosion different fragments fly in various directions. It will be observed that their momenta, when represented by the slide of a polygon, from a closed polygon, indicating that net momentum after explosion is also zero. Thus, if the bomb exploded into two fragments, they must move in opposite directions.
(d) A man Jumping from a Boat
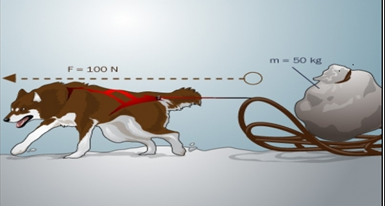
When a man jumps from the boat to the shore, the boat is pushed backward. It can, exactly, be explained as in the case of recoil of gun.
Some Conceptual Questions
Question 1:-
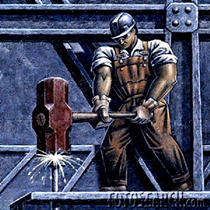
Figure below shows a popular carnival device, in which the contestant tries to see how high a weighted marker can be raised by hitting a target with a sledge hammer. What physical quantity does the device measure? Is it the average force, the maximum force, the work done, the impulse, the energy transferred, the momentum transferred, or something else? Discuss your answer.
Answer:-
The device will measure impulse. The impulse of the net force acting on a particle during a given time interval is equal to the change in momentum of the particle during that interval. Since the contestant is hitting the target with a sledge hammer the change in momentum is large and the time of collision is small, therefore it signifies that the average impulsive force will relatively large. Suppose two persons bring the harmer from the same height, but they are hitting with different forces. The person who hits with greater force for the short time interval the impulse will be more and this results the height of the mark will be more. Thus the device will measure impulse.
________________________________________________________________________________________________________________
Question 2:-
Can the impulse of a force be zero, even if the force is not zero? Explain why or why not?
Answer:-
Yes, the impulse of a force can be zero, even if the force is not zero.
Impulse of a force is defined as the change in momentum produced by the force and it is equal to the product of force and the time for which it acts. The impulse of a force can be zero, if the net force acting on the particle during that time interval is constant. Since the force is constant (both magnitude and direction), so change in momentum produced by the force will be zero. Therefore impulse of the force will be zero.
From the above observation we conclude that, impulse of a force can be zero, even if the force is not zero.
__________________________________________________________________________________________________________________
Question 3:-
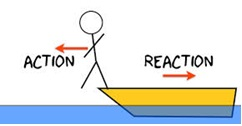
Explain how conservation of momentum applies to a handball bouncing off a wall.
Answer:-
Law of conservation of linear momentum states that, in an isolated system (no external force), the algebraic sum of momenta of bodies, along any straight line, remains constant and is not changed due to their mutual action and reaction on each other.
The momentum of particle (p) is equal to the mass of particle (m) times the velocity of particle (v).
So,p = mv …… (1)
Let us consider m is the mass of the ball and v is the velocity of the ball when the ball is collides with wall.
So using equation (1), the momentum of the ball before collision (p1) will be,
p1= mv …… (2)
After collision, when the ball re bounces, the velocity of the ball will be, -v.
So again using equation (1), the momentum of the ball after collision (p2) will be,
p2= -mv …… (3)
Conservation of linear momentum states that, the algebraic sum of momenta of bodies, along any straight line, remains constant and is not changed due to their mutual action and reaction on each other.
p1 + p2 = 0
So, mv + (-mv) = 0 …… (4)
From equation (4) we observed that, linear momentum of the hand ball is conserved.
_________________________________________________________________________________________________________
Question 4:-
Give a plausible explanation for the breaking of wooden boards or bricks by a karate punch. (See “Karate Strikes.” by Jearl D. Walker, American Journal of Physics, October 1975, p.845.)
Answer:-
In the process, breaking of wooden boards or bricks by a karate punch, the collision between the hand and brick is only for a few milliseconds. Because the applied external force is large and the time of collision is small therefore the average impulsive force is relatively large. Thus when you break a wooden board or bricks by a karate punch you have to apply large force for the minimum time which is impulse. Therefore the impact force on the brick or wooden boards will be high.
Some Solved Problems
Problem 1:-
A 75.2-kg man is riding on a 38.6-kg cart travelling at a speed of 2.33 m/s. He jumps off in such a way as to land on the ground with zero horizontal speed. Find the resulting change in the speed of the cart.
Concept:-
Momentum of the body p is equal to the mass of the body m times velocity of the body v.
So, p = mv
In accordance to the principle of conservation of energy, the final momentum of the system is equal to the initial momentum of the system.
Consider the initial momentum of the man is pi,m, initial momentum of the cart is pi,c, final momentum of the man is pf,m and final momentum of the cart is pf,c.
We define, pf,m = mmvf,m
pf,c = mcvf,c
pi,m = mmvi,m
pi,c = mcvi,c
Here, mass of the man is mm, mass of the cart is mc, initial velocity of the man is vi,m and cart is vi,c, and final velocity of the man is vf,m and cart is vf,c.
Solution:-
So applying conservation of momentum to this system, the sum of the initial momentum of the man and cart will be equal to the sum of the final momentum of the man and cart.
pf,m + pf,c = pi,m + pi,c
Substitute, mmvf,m for pf,m, mcvf,c for pf,c, mmvi,m for pi,m and mcvi,c for pi,c ijn the equation pf,m + pf,c = pi,m + pi,c,
pf,m + pf,c = pi,m + pi,c
mmvf,m + mcvf,c = mmvi,m + mcvi,c
vf,c- vi,c = (mmvi,m - mmvf,m)/ mc
Δvc = (mmvi,m - mmvf,m)/ mc
To obtain the resulting change in the speed of the cart Δvc, substitute 75.2 kg for mm, 2.33 m/s for vi,m and 0 m/s for vf,m in the equation Δ vc = (mmvi,m - mmvf,m)/ mc,
Δvc = (mmvi,m - mmvf,m)/ mc
= (75.2 kg) (2.33 m/s) – (75.2 kg) (0 m/s)/(38.6 kg)
= 4.54 m/s
As the sign of the change in the speed of the cart Δvc is positive, this signifies that, the cart speed increases.
From the above observation we conclude that, the resulting change in the speed of the cart Δvc would be 4.54 m/s.
___________________________________________________________________________________________________________
Problem 2:-
A space vehicle is travelling at 3860 km/h with respect to the Earth when the exhausted rocket motor is disengaged and sent backward with a speed of 125 km/h with respect to the command module. The mass of the motor is four times the mass of the module. What is the speed of the command module after the separation?
Concept:-
Momentum of the body p is equal to the mass of the body m times velocity of the body v.
So, p = mv
In accordance to the principle of conservation of energy, the final momentum of the system is equal to the initial momentum of the system.
Consider the initial momentum of the motor is pi,m, initial momentum of the command module is pi,c, final momentum of the motor is pf,m and final momentum of the command module is pf,c.
Initial momentum of the motor is equal to the initial momentum of the command module.
So, initial momentum of the motor will be,
pi,m = mmvi,c
and final momentum of the motor pf,m will be,
pf,m = mm(vf,c – vrel)
Here, speed of the motor relative to the command module is vrel.
Again, pf,c = mcvf,c
pi,c = mcvi,c
Here, mass of the motor is mm, mass of the command module is mc, initial velocity of the motor is vi,m and command module is vi,c, and final velocity of the motor is vf,m and command module is vf,c.
Solution:-
So applying conservation of momentum to this system, the sum of the initial momentum of the motor and command module will be equal to the sum of the final momentum of the motor and command module.
pf,m + pf,c = pi,m + pi,c
Substitute, mm(vf,c – vrel) for pf,m, mcvf,c for pf,c, mmvi,c for pi,m and mcvi,c for pi,c in the equation pf,m + pf,c = pi,m + pi,c,
pf,m + pf,c = pi,m + pi,c
mm(vf,c – vrel)+ mcvf,c = mmvi,c + mcvi,c
(mm + mc)vf,c - mm vrel = (mm +mc) vi,c
(mm + mc)vf,c = mm vrel + (mm +mc) vi,c
So, vf,c = [mm vrel + (mm +mc) vi,c]/ (mm + mc)
As, mass of the motor is four times the mass of the module, thus,
mm = 4 mc
To obtain the speed of the command module vf,c, substitute 4 mc for mm, 125 km/h for vrel and 3860 km/h for vi,c in the equation vf,c = [mm vrel + (mm +mc) vi,c]/ (mm + mc),
vf,c = [mm vrel + (mm +mc) vi,c]/ (mm + mc)
= [4 mc(125 km/h) + (4 mc+mc) (3860 km/h)]/ [4 mc+ mc]
= 3960 km/h
From the above observation we conclude that, the speed of the command module vf,c would be 3960 km/h.
Work, Energy and Power:-
Work, Energy and power are some of the more important topics of mechanics in classical physics.
A car moving, a rocket taking off, an aero plane flying, are a few of the events which take place regularly and can give us insight into the concept of Work and Energy. These are some of the common sense notions of work and energy - which can however be precisely defined and measured in physics.
These definitions and measurement can be used consistently to describe and predict the behavior of bodies.
Work is related to energy as they are inter-convertible and also the sums of them are conserved in Newtonian Physics. Power is a step further which defines the rate of change of energy flow.The examples based on this are very easy and can be seen even in day to day life.
Work:-
Work is said to be done if a force, acting on a body, displaces the body through a certain distance and the force has some component along the displacements. Thus, work is done when the point of application of a force moves.It is defined as the product of magnitude of displacement and the component of the force along the displacement.
Power:-
The rate at which work is done is called power.
Energy:-
Energy is the ability of the body to do some work. The unit of energy is same as that of work.
The chapter is important not only because it fetches 3-4 questions in most of the engineering examination but also because it is like a linking pin to the previous and other forthcoming chapters of Mechanics.
Following Study material topics are covered under Work, Energy and Power:-
Work, Energy and Power is one of the topics which you can never afford to ignore, no matter which competitive examination you are preparing for. The concepts need to be understood well as this will give a smooth entry to the next few chapters of Mechanics. This chapter is key to many of the examination including IIT JEE, AIEEE, AICET, DCE and EAMCET in particular.
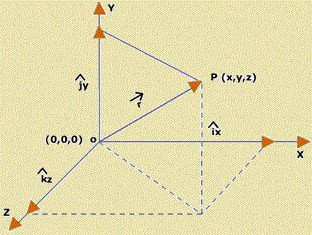
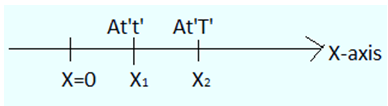
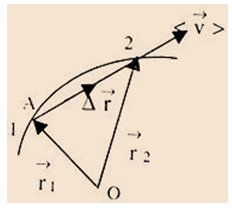

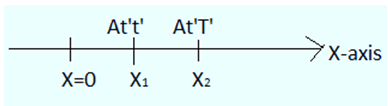
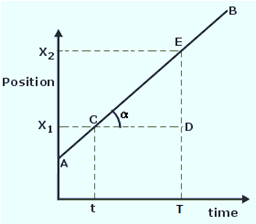
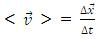
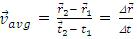
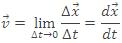
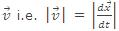
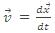
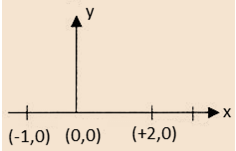
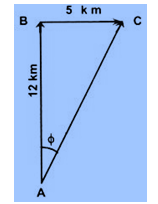


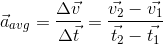
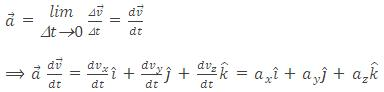
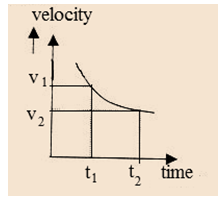
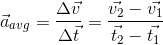
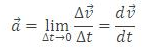
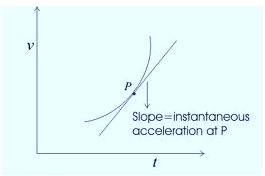
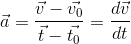
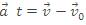
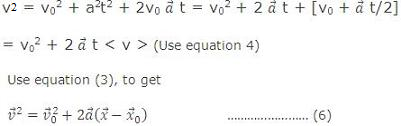

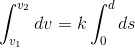
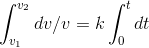




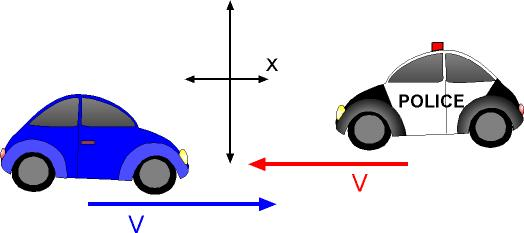
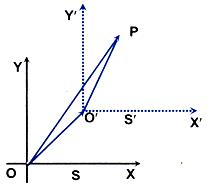
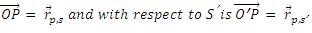
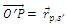
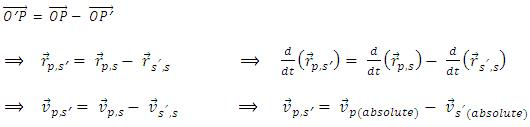
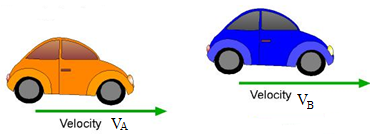
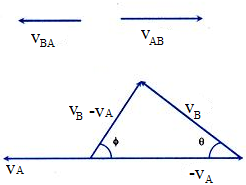

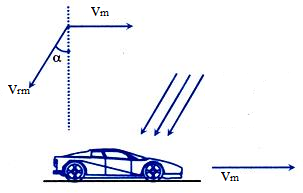
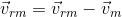
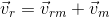
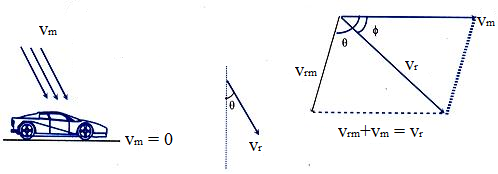
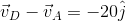

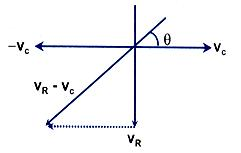
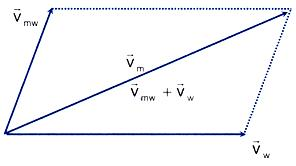
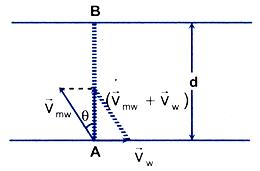
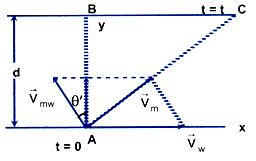
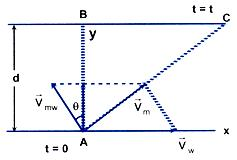
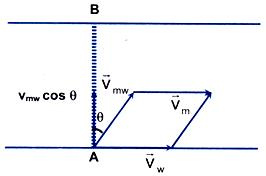
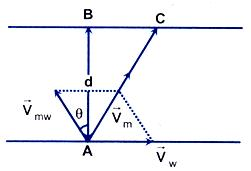
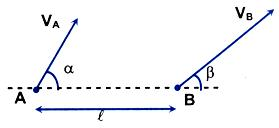


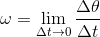
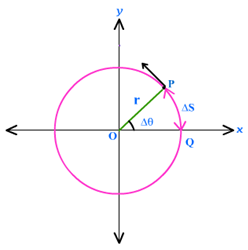
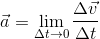
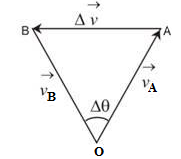
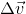
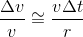
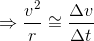
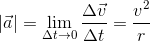
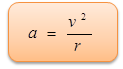
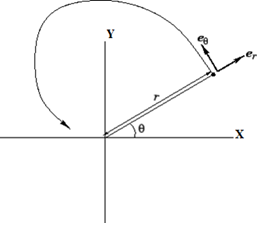
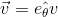
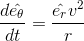
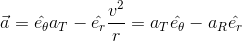






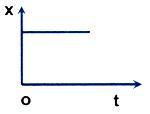
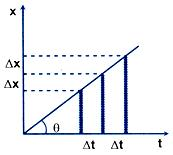
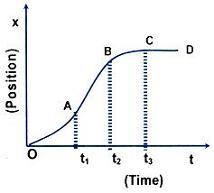
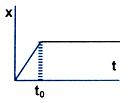
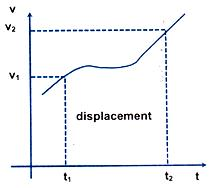
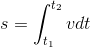
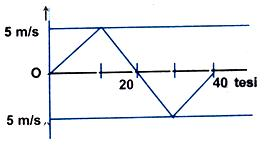
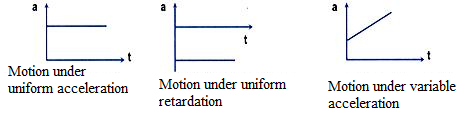






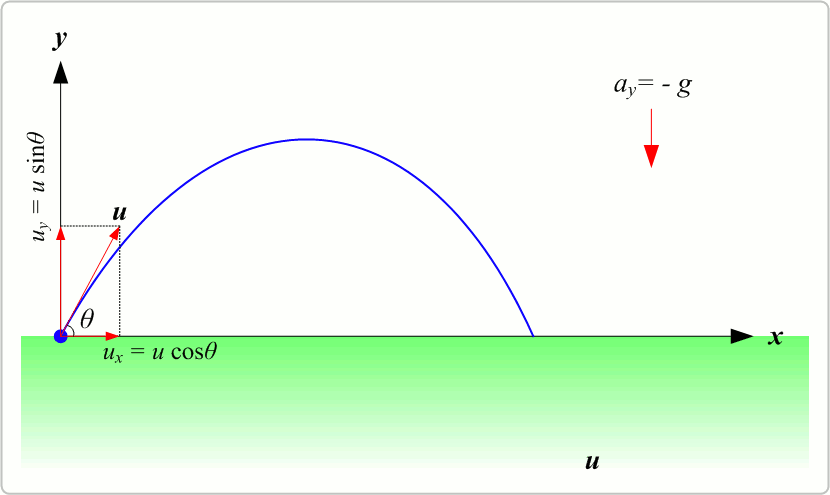
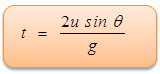

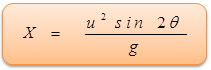
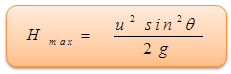
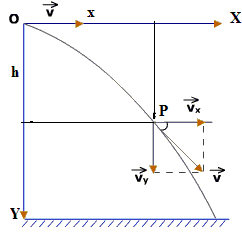
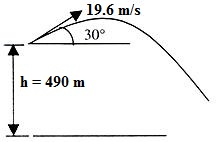
![t = \frac{2\pm \sqrt{(2^{2}-4\times 1\times \left [ -100 \right ])}}{2\times 1} =1+\sqrt{101}](https://static.s123-cdn-static-c.com/uploads/1269728/2000_5b41bb554269d.jpg)